斐波那契数列
求解斐波那契数列是一道经典的算法问题，本文在总结常规解法的基础上，进一步探讨算法的优化方法。
斐波那契数列的定义
我们定义满足如下表达式的数列为斐波那契数列：
$f(n) = 1 ~~~n=1,2$
$f(n) = f(n-1)+f(n-2) ~~~n>2$
递归方法
我们根据表达式，可以很快用递归的方法写出代码：
#include <stdio.h>
#include<time.h>
unsigned long fibonacci(int n);
int main(void) {
clock_t start, finish;
unsigned long result;
int n = 30;
start=clock();
result = fibonacci(n-1);
finish = clock();
printf("%lu\n", result);
printf("%lf s\n", (double)(finish - start)/CLOCKS_PER_SEC);
return 0;
}
unsigned long fibonacci(int n) {
if (n < 2)
return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
| n | 运行时间（秒） |
|---|---|
| 30 | 0.002975 |
| 40 | 0.392288 |
| 50 | 45.450654 |
可见随着 n 的增加，程序所需时间急速增加。
性能分析
递归算法虽然很简洁，但在时间复杂度和空间复杂度上存在巨大的缺陷。
我们由斐波那契数列的递推公式可得：
$$T(n) = T(n-1) + T(n-2)~~~~~S(n) = S(n-1)+S(n-2)$$
使用差分方程，我们可以求得：
$$T(n) \sim O(k^n) ~~~~ S(n) \sim O(k^n) ~~~~ k =\frac{1+\sqrt{5}}{2} \approx 1.62$$
由于 $k > 1$，当 n 增大时，程序所需的时间和空间都会指数级的上升。我们可以看一下系统的栈空间限制：
$ ulimit -s
8192
当 n 足够大时，可能出现内存溢出。
动态规划
我们将每次计算的结果保存在一个数组中，这样我们省略大量重复的计算，具体代码如下：
#include <stdio.h>
#include<time.h>
#include <stdlib.h>
unsigned long fibonacci(int n, unsigned long *array);
int main(void) {
clock_t start, finish;
unsigned long result, *array;
int n = 1000;
start=clock();
array = malloc(sizeof(unsigned long) * (n-1));
result = fibonacci(n-1, array);
finish = clock();
printf("%lu\n", result);
printf("%lu s\n", finish - start);
free(array);
array = NULL;
return 0;
}
unsigned long fibonacci(int n, unsigned long *array) {
if (n < 2)
array[n] = 1;
else
array[n] = fibonacci(n-1, array) + array[n-2];
return array[n];
}
n = 10000时，仅需要 245μs，此时算法的时间复杂度和空间复杂度均减少到了 $O(n)$。
尾递归
此时时间复杂度已经很好，但考虑到每次递归都会在栈空间上开辟一块空间，用来调用函数，我们可以用尾递归的方式对空间复杂度做进一步的优化。
#include <stdio.h>
#include<time.h>
unsigned long fibonacci(int n, unsigned long f1, unsigned long f2);
int main(void) {
clock_t start, finish;
unsigned long result;
int n = 10000;
start=clock();
result = fibonacci(n, 1, 1);
finish = clock();
printf("%lu\n", result);
printf("%lu μs\n", finish - start);
return 0;
}
unsigned long fibonacci(int n, unsigned long f1, unsigned long f2) {
if (n == 1)
return f2;
else
return fibonacci(--n, f1+f2, f1);
}
通过尾递归，虽然时间复杂度不变，但空间复杂度降至 $O(1)$。n = 10000时，时间为 234μs。
循环
我们可以直接用循环计算斐波那契数列，避免大量的函数调用开销，代码为：
#include <stdio.h>
#include<time.h>
int main(void) {
clock_t start, finish;
start = clock();
unsigned long pre = 1, result = 1, media;
int i, n = 10000;
for (i = 0; i < n-2; i++) {
media = pre;
pre = result;
result += media;
}
finish = clock();
printf("%lu\n", result);
printf("%lu μs\n", finish - start);
return 0;
}
此时时间复杂度为 $O(n)$，空间复杂度为 $O(1)$，n = 10000时，运行时间直接降至 25μs。
矩阵分解计算
到了这里，单纯的使用算法很难再进一步优化性能。因此我们使用数学的方法，对斐波那契数列的表达式进行优化。我们将他的递推公式写成矩阵的形式：
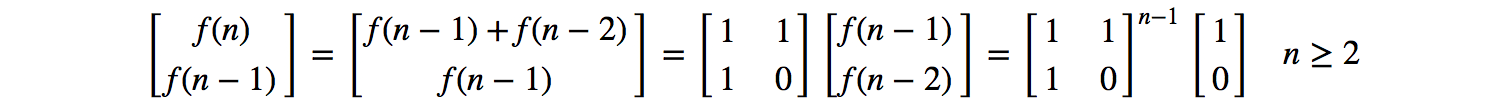接下来，我们的问题就是如何快速的求解变换矩阵的n-1次方，这里我们可以对矩阵进行特征分解。
特征分解
我们首先回顾下特征值和特征向量的定义：
$$Ax = \lambda x$$
A 为 $ n \times n$ 的矩阵，x是一个 n 维向量，$\lambda$ 是一个常数。这个表达式的几何意义是，对向量 x 做空间变换 A，仅仅缩放 x 的模，并不改变 x 在空间中的角度。
我们求出矩阵 A 的 n 个特征值 $\lambda_1,…,\lambda_n$，以及对应的特征向量 $x_1,…,x_n$，我们可以将矩阵 A 写成如下形式：
$$A = W\Sigma W^{-1} = [x_1,…,x_n] diag(\lambda_1,…,\lambda_n) [x_1,…,x_n]^{-1} $$
此时我们可以很方便的计算 A 的 n 次方：
$$A^{n} = W\Sigma^n W^{-1} = Wdiag(\lambda_1^n,…,\lambda_n^n) W^{-1}$$
现在，我们求解变换矩阵的特征值和特征向量：
$\lambda(\lambda-1)-1 = 0 ~~~ \rightarrow ~~\lambda_1=\frac{1+\sqrt{5}}{2} ~~~\lambda_2 = \frac{1-\sqrt{5}}{2}$
$w_1 = [1, \frac{\sqrt{5}-1}{2}]^{\top}~~~~~w_2=[1, -\frac{\sqrt{5}+1}{2}]^{\top}$
将以上式子代入最初的表达式，我们可以求得斐波那契数列的表达式：
$$f(n) = \frac{1}{\sqrt{5}} [(\frac{1+\sqrt{5}}{2})^n - (\frac{1-\sqrt{5}}{2})^n]$$
代码如下
#include <stdio.h>
#include <math.h>
#include<time.h>
int main(void) {
clock_t start, finish;
start = clock();
unsigned long result;
int n = 10000;
if (n <= 2)
result = 1;
result = (unsigned long)((pow((1+sqrt(5))/2,n)-pow((1-sqrt(5))/2,n))/sqrt(5));
finish = clock();
printf("%lu\n", result);
printf("%lu μs\n", finish - start);
return 0;
}
当 n = 10000 时，耗时仅为 11μs。