信息熵和互信息

本文主要总结了信息熵在信息论中的具体意义，并介绍了互信系数，最后简单整理了MIC（最大互信系数）的内容和具体用法。

信息熵的定义

我们考虑一个离散的随机变量x。当我们观察到这个变量的一个具体值的时候，我们接收到了多少信息呢。我们对于信息内容的度量将依赖于概率分布p(x)，因此我们想要寻找一个函数h(x)，它是概率p(x)的单调递减函数，表达了信息的内容。

$h(·)$形式可以这样寻找:如果我们有两个不相关的事件x和y，那么我们观察到两个事件同时发生时获得的信息应该等于观察到事件各自发生时获得的信息之和，即$h(x, y) = h(x) + h(y)$。因为$p(x, y) = p(x)p(y)$，很容易看出h(x)一定与p(x)的对数有关。同时为了保证$h(x) > 0$，设置：

$$h(x) = -log(p(x))$$

现在假设一个发送者想传输一个随机变量的值给接收者。这个过程中，他们传输的平均信息量的期望值这个期望值为：

$$H(x) = \sum p(x)h(x) = -\sum p(x)log(p(x))$$

从信息学角度看信息熵

熵的定义在信息学上有实际的应用性质

考虑一个随机变量x。这个随机变量有8种等可能的状态，用二进制来标识x的不同状态，为了把x的值传给接收者，我们需要传输一个3bit的消息。

$H(x) = -8 \times \frac{1}{8}log_2(\frac{1}{8}) = 3$

如果这8种状态不是等可能的呢？

如果8种状态不是等可能的，那么用3bit长度的编码来标识不同的状态不是最理想的编码方式。可以调整编码的格式对信息进行压缩，让出现频率高的状态使用长度较短的编码。

使用霍夫曼编码对信息进行压缩：

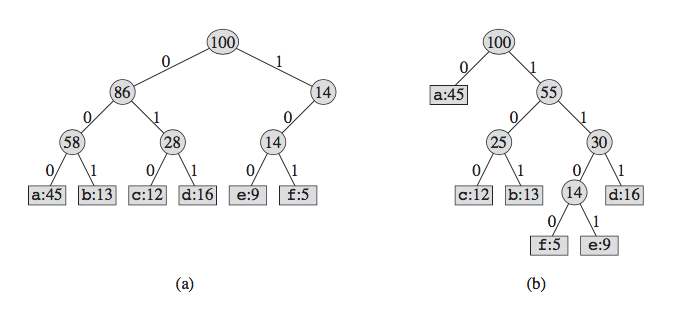
huffamn coding

无噪声编码定理：编码的期望长度不小于随机变量的信息熵。

从概率论的角度看信息熵

考虑一个集合，包含N个完全相同的物体，这些物体要被分到若干个箱子中，使得第i个箱子中有$n_i$个物体。

把N个物体分配到箱子中的总方案数量为:

$$W = \frac{N!}{\prod_i n_i!}$$

$H = \frac{\ln W}{N}= \frac{1}{N}\ln N! - \frac{1}{N}\sum_i \ln n_i!$

$N \rightarrow \infty, \ln N! \approx N\ln N - N$

$H = \lim_{N \to \infty} \frac{\ln W}{N} = \ln N - 1 - \sum(\frac{n_i}{N}\ln n_i - \frac{n_i}{N})$

$~~~=-\sum\frac{n_i}{N}\ln \frac{n_i}{N} = -\sum p_i \ln p_i$

相对熵和互信息

考虑某个未知的分布p(x)，假定我们已经使用一个近似的分布q(x)对它进行了建模。由于我们使用了q(x)而不是真实分布p(x)，因此我们需要附加一些信息，而附加信息的量：

$$KL(p||q) = -\int p(x)\ln q(x)dx + \int p(x)\ln p(x)dx = -\int p(x)\ln \frac{p(x)}{q(x)}dx \geq 0$$

KL散度看做两个分布p(x)和q(x)之间不相似程度的度量，当q(x)和p(x)相同时KL散度为零。

现在我们另$p = p(X,Y), q = p(X)p(Y)$ 根据独立性的性质，我们可知，当X与Y独立时，$p(X,Y) = p(X)p(Y)$ 我们想知道X,Y的独立性

$$I(X;Y) = KL(p(X,Y)||p(X)p(Y)) = \int_X\int_Y p(X,Y) \log \frac{p(X,Y)}{p(X)p(Y)}$$

我们可以从编码压缩的角度理解KL散度，当我们知道真实的概率分布之后，我们可以给出最有效的压缩。如果我们使用了不同于真实分布的概率分布，那么我们一定会损失编码效率。

接下来，我们先来看一下互信息(Mutual Information)。

假设存在随机变量$x,y$, 我们可以用$R^2$来衡量两个变量之间的线性相关程度，但当随机变量之间的函数关系非线性时，我们就必须用其他方法考察他们之间的独立性。

根据独立性的性质，我们可知，当X与Y独立时，$p(X,Y) = p(X)p(Y)$，我们定义互信息MI:

$$I(X;Y) = \int_X\int_Y p(X,Y) \log \frac{p(X,Y)}{p(X)p(Y)}$$

下面我们对$I(X;Y)$进行一定的变形：

$I(X;Y) = \int_X\int_Y p(X,Y) \log \frac{p(X,Y)}{p(X)p(Y)}$

$~~~~~~~~~~~=\int_X\int_Y p(X,Y)\log\frac{p(X,Y)}{p(X)} - \int_X\int_Y p(X,Y)\log p(Y)$

$~~~~~~~~~~~=\int_X\int_Y p(X)p(Y|X)\log p(Y|X) - \int_y p(Y)\log p(Y)$

$~~~~~~~~~~~=\int_X p(X)\int_Yp(Y|X)\log p(Y|X)+H(Y)$

$~~~~~~~~~~~=-\int_X p(X)H(Y|X=x)+H(Y)$

$~~~~~~~~~~~=H(Y)-H(Y|X)$

因此$I(X;Y)$显示了X的引入对于Y的熵的减少量，因而当X和Y独立时，$H(Y)=H(Y|X), I(X;Y)=0$

MIC

MIC(Maximal information coefficient) 最早源自于2011年发表于science上的论文-Detecting Novel Associations in Large Data Sets.是一种衡量两个随机变量之间独立性的参数方法。

假设存在随机变量$X,Y$, 我们可以用$Cov(X,Y)$来衡量两个变量之间的线性相关程度，但当随机变量之间的函数关系非线性时，$Cov(X,Y)$我发准确的反映变量之间的相关性，我们就必须用其他方法考察他们的独立性。

具体方法

假设我们拿到了随机变量$X,Y$的散点图，我们用小方格子去分割图形，保证在每个小方格子里$I(X;Y)$最大，然后对每个网格中$I(X;Y)$进行归一化处理。选取所有$I(X;Y)$中的最大值作为MIC，注意网格数量应小于$n^{0.6}$。

$$MIC(X;Y) = \max\frac{I(X;Y)}{\log_2(\min(|X|,|Y|))}$$

MIC

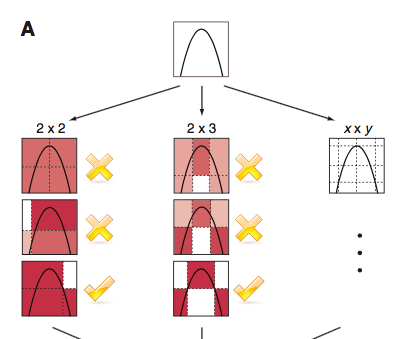
实际应用

我们可以使用minepy库，来计算随机变量的MIC。先做一条sin曲线，计算一下x,y之间的MIC。接着，我们在y上加入噪声信号，重新计算MIC。

import numpy as np
from minepy import MINE
import matplotlib.pyplot as plt

x = np.linspace(0, 1, 1000)
y = np.sin(10 * np.pi * x) + x 
noise = y + np.random.random(1000)

mine = MINE(alpha=0.6)
mine.compute_score(x, y)      # mine.mic() = 1
mine.compute_score(x, noise)  # mine.mic() = 0.81

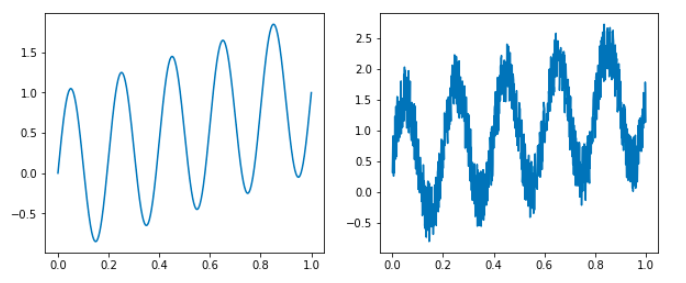
MIC_figure

我们可以看到，对于sin曲线的x和y，MIC为1（相关度极高），即使加入噪音进行干扰，MIC依然有0.81。

接下来我们看看MIC对完全独立的随机数的表现。

x = np.random.random(1000)
y = np.random.random(1000)
mine = MINE(alpha=0.6)
mine.compute_score(x, y) # mine.mic() = 0.137